O problema do matemático medieval Leonardo Fibonacci sobre os coelhos

Vamos ver como o número de coelhos cresce nos primeiros seis meses:

Mês 1. Um par de coelhos jovens.

Mês 2. Ainda existe um par original. Os coelhos ainda não atingiram a idade reprodutiva.

Mês 3. Dois pares: o original, que atingiu a idade fértil, + um par de coelhos jovens que ela deu à luz.

4º mês. Três pares: um par original + um par de coelhos que ela deu à luz no início do mês + um par de coelhos que nasceu no terceiro mês, mas ainda não atingiu a maturidade sexual.

5º mês. Cinco pares: um par original + um par nascido no terceiro mês e em idade fértil + dois novos casais que deram à luz + um casal, que nasceu no quarto mês, mas ainda não atingiu maturidade.

6º mês. Oito casais: cinco casais do mês passado + três casais recém-nascidos. Etc.

Para deixar mais claro, vamos escrever os dados recebidos na tabela:

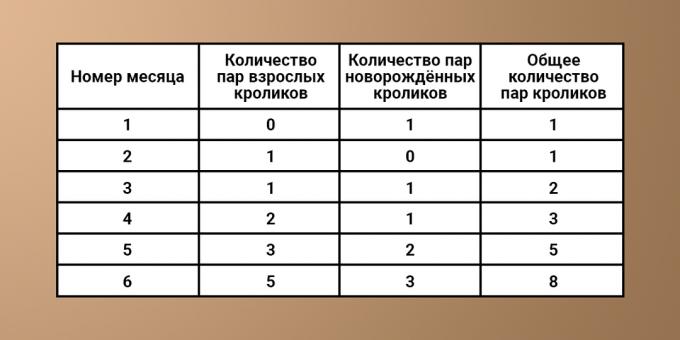
Se você examinar cuidadosamente a tabela, poderá identificar o seguinte padrão. Cada vez que o número de coelhos presentes no enésimo mês é igual ao número de coelhos no (n - 1) o mês anterior, somado ao número de coelhos recém-nascidos. Seu número, por sua vez, é igual ao número total de animais no (n - 2) mês (que foi há dois meses). Daqui você pode deduzir

Fórmula:

F_n = F_{n - 1}+ F_{n - 2},

onde F_n - o número total de pares de coelhos no enésimo mês, F_{n - 1} É o número total de pares de coelhos no mês anterior, e F_{n - 2} - o número total de pares de coelhos há dois meses.

Vamos contar o número de animais nos meses seguintes usando:

7º mês. 8 + 5 = 13.

8º mês. 13 + 8 = 21.

9º mês. 21 + 13 = 34.

Mês 10. 34 +21 = 55.

11º mês. 55 + 34 = 89.

12 meses. 89 + 55 = 144.

Mês 13 (início do próximo ano). 144 + 89 = 233.

No início do 13º mês, ou seja, no final do ano, teremos 233 pares de coelhos. Destes, 144 casais serão adultos e 89, jovens. A sequência resultante 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 chamados de números de Fibonacci. Nele, cada novo número final é igual a soma os dois anteriores.