Aquecimento para o cérebro: você pode resolver o problema da moeda falsificada? Confira!

O matemático tem apenas três tentativas, então você não pode pesar cada moeda separadamente. É preciso dividi-los em pilhas e colocá-los na balança várias peças de cada vez, aproximando-se gradativamente da falsa.

Digamos que um matemático decida dividir 12 moedas em três pilhas de quatro moedas cada. Em seguida, ele colocou quatro moedas em cada escala. Essa pesagem pode dar dois resultados. Vamos considerar cada um deles.

1. O peso das duas pilhas de moedas era o mesmo. Consequentemente, todo o dinheiro nelas é real e a falsificação está em algum lugar entre as quatro moedas não ponderadas.

Para rastrear o resultado, o matemático marca todos os scripts com um zero. Então ele pega três delas e as compara com três moedas não pesadas. Se o peso for igual, a (quarta) moeda restante não ponderada é falsificada. Se o peso for diferente, o matemático coloca um sinal de mais nas três moedas não marcadas se elas forem mais pesadas do que aquelas com zeros, ou um sinal de menos se elas forem mais leves.

Então ele pega dois moedasmarcada com mais ou menos e compara seu peso. Se for o mesmo, a cópia restante é falsa. Do contrário, o matemático olha para os sinais: entre as moedas com mais, a falsa será a mais pesada, entre as moedas com menos, a mais leve.

2. O peso das duas pilhas de moedas não era o mesmo.

Nesse caso, o matemático precisa agir da seguinte forma: marcar o dinheiro em uma pilha pesada com um sinal de mais, em uma pilha leve - com um sinal de menos, em uma pilha não ponderada - com um zero, pois se sabe que a cópia falsa estava na balança.

Agora você precisa reagrupar as moedas para caber nas duas pesagens restantes. Uma das maneiras é pegar em vez de três moedas com um mais, três moedas com um menos e colocar três peças com um zero em seu lugar.

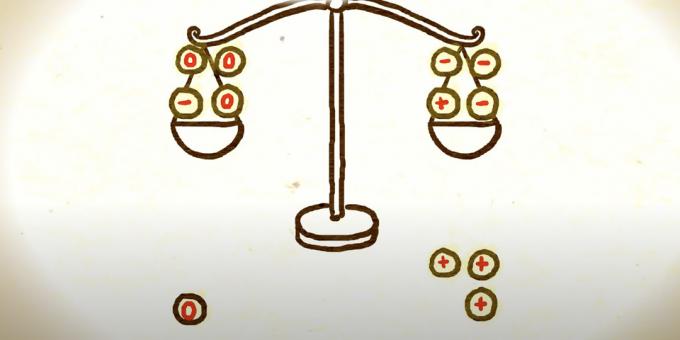
Seguem três opções possíveis. Se a escala que era mais pesada ainda supera o peso, então ou a moeda antiga com o sinal de mais nela é mais pesada do que o resto, ou a moeda com o sinal de menos restante na outra escala é mais leve. Um matemático precisa escolher qualquer um deles e comparar com um padrão comum para encontrar um falso.

Se o prato de pesagem, que era mais pesado, ficou mais leve, então uma das três moedas com o sinal menos movidas pelo matemático é a mais leve. Agora ele precisa comparar dois deles na balança. Se os resultados estiverem empatados, a terceira moeda será falsificada. Em caso de desigualdade, o falso é mais fácil.

Se as tigelas forem equilibradas após a recolocação, uma das três moedas removidas da balança com um sinal de mais é mais pesada que as outras. Um matemático precisa comparar dois deles. Se eles forem iguais, o terceiro é falso. Com a desigualdade, o mais pesado não é real.

O imperador acena com a cabeça em aprovação enquanto ouve o raciocínio Matemáticas, mas o governador desonesto vai para a prisão.

Este quebra-cabeça é a tradução de um vídeo TED-Ed.